
這段時間在學習一個好用的技巧 – Isolation Lemma. 當我們需要在一個圖中找到特定的結構 (例如一個 perfect matching), 有時直接去找不是那麼容易; 藉由孤立 (isolation) 出某一個特定的 minimum weighted matching, 我們就能很快的找到它. 最有名的使用就是在 [MVV87] 中 Mulmuley, Vazirani 和 Vazirani (你沒看錯) 藉由證明了最初 Isolation Lemma 的雛形而得到的 perfect matching (平行) 演算法.
(平行) 演算法.
在此我們介紹兩種不同的改良版: 一種是後來被 [RA00] 使用, Reinhardt 和 Allender 證明了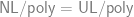 ; 此種方法的特點是得到的 bound 很好, 但是是非建構式的. 而另一種類似 hash 的方式則是被 [CRS93] 使用, 改進了當初 [MVV87] 的演算法而得的
; 此種方法的特點是得到的 bound 很好, 但是是非建構式的. 而另一種類似 hash 的方式則是被 [CRS93] 使用, 改進了當初 [MVV87] 的演算法而得的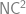 perfect matching 演算法; 後面這種方法 weight 是建構式的, 可以直覺的看出為何它能夠把所有東西分開, 但是要用到少許的 randomization. (嚴格來說, 我們真正要使用第一種方式時, 還是有 randomized 的精神在裡頭.)
perfect matching 演算法; 後面這種方法 weight 是建構式的, 可以直覺的看出為何它能夠把所有東西分開, 但是要用到少許的 randomization. (嚴格來說, 我們真正要使用第一種方式時, 還是有 randomized 的精神在裡頭.)
—
首先我們來看第一個形式的 Isolation Lemma.
Theorem 1. 令 為一大小為
為一大小為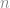 的集合, 而
的集合, 而 為一族非空集合, 其中每一
為一族非空集合, 其中每一 為
為 的子集所形成的集合. 令
的子集所形成的集合. 令 為重量的上限, 而
為重量的上限, 而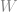 為所有重量不超過
為所有重量不超過 的重量函數
的重量函數![w: U \rightarrow [d]^n](https://s0.wp.com/latex.php?latex=w%3A+U+%5Crightarrow+%5Bd%5D%5En&bg=ffffff&fg=777777&s=0&c=20201002) 形成的集合. 若我們給定一參數
形成的集合. 若我們給定一參數 使得
使得 , 則至少有
, 則至少有 的重量函數會使得每個
的重量函數會使得每個 中正好都只有一個最小重量的
中正好都只有一個最小重量的 子集.
子集.
看起來很複雜. 我們令 ,
,  和
和 來觀察這個定理看看.
來觀察這個定理看看.
Theorem 1′. 令 為一大小為
為一大小為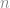 的集合, 而
的集合, 而 為一非空集合,
為一非空集合,  中每一元素為
中每一元素為 的子集. 均勻獨立的在
的子集. 均勻獨立的在 上隨機給定
上隨機給定![[2n]](https://s0.wp.com/latex.php?latex=%5B2n%5D&bg=ffffff&fg=777777&s=0&c=20201002) 內的重量. 則至少有
內的重量. 則至少有 的機率會使得
的機率會使得 中正好只有一個最小重量的
中正好只有一個最小重量的 子集.
子集.
這樣就好懂多了; 藉由隨機給定一些不大的重量, 很容易能夠使得 中有個最小元素被孤立出來. 如果不要限制重量的大小, 這其實不是很困難; 只要對
中有個最小元素被孤立出來. 如果不要限制重量的大小, 這其實不是很困難; 只要對 中的元素
中的元素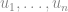 分別給予重量
分別給予重量 就行了. 不難根據二進位表示看出
就行了. 不難根據二進位表示看出 中的元素都會有不同的重量. 重點在於, 這樣的重量是指數成長的, 而多數演算法的應用只能限制在多項式成長率下. 這時藉由一點點的隨機性, 就能夠達成這樣的目標, 這是 Isolation Lemma 的厲害之處!
中的元素都會有不同的重量. 重點在於, 這樣的重量是指數成長的, 而多數演算法的應用只能限制在多項式成長率下. 這時藉由一點點的隨機性, 就能夠達成這樣的目標, 這是 Isolation Lemma 的厲害之處!
來看一個實際的例子好了. 在 [RA00] 的證明當中, 他們用 Isolation Lemma 孤立出圖中某兩點之間的某條路徑. 因為對任意圖來說兩點間的路徑最多會有 exponential 那麼多, 所以我們需要借助 Isolation Lemma.
令![[p]](https://s0.wp.com/latex.php?latex=%5Bp%5D&bg=ffffff&fg=777777&s=0&c=20201002) 為圖中的點集,
為圖中的點集,  為圖中的邊集,
為圖中的邊集,  為點
為點 到點
到點 所有路徑的集合. (注意我們將路徑視為邊集的子集.) 因為
所有路徑的集合. (注意我們將路徑視為邊集的子集.) 因為 (有向邊), 我們令
(有向邊), 我們令 ,
,  ,
,  . 因此根據 Theorem 1, 我們可以證明底下的推論:
. 因此根據 Theorem 1, 我們可以證明底下的推論:
Corollary. 令 為一
為一 點有向圖, 而
點有向圖, 而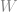 為所有重量函數
為所有重量函數![w: E(G) \rightarrow [2p^3]^n](https://s0.wp.com/latex.php?latex=w%3A+E%28G%29+%5Crightarrow+%5B2p%5E3%5D%5En&bg=ffffff&fg=777777&s=0&c=20201002) 形成的集合. 則至少有
形成的集合. 則至少有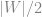 的重量函數會使得對於所有
的重量函數會使得對於所有 , 點
, 點 到點
到點 的最小重量路徑是唯一的.
的最小重量路徑是唯一的.
為什麼需要這麼多的重量函數呢? 因為我們可以藉此證出更厲害的推論:
Corollary. 令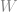 為所有重量函數
為所有重量函數![w: E(G) \rightarrow [2p^3]^n](https://s0.wp.com/latex.php?latex=w%3A+E%28G%29+%5Crightarrow+%5B2p%5E3%5D%5En&bg=ffffff&fg=777777&s=0&c=20201002) 形成的集合. 則存在
形成的集合. 則存在 個重量函數會使得對於所有
個重量函數會使得對於所有 點有向圖
點有向圖 , 一定有一個
, 一定有一個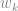 使得在
使得在 種任意點
種任意點 到點
到點 的最小重量路徑是唯一的.
的最小重量路徑是唯一的.
Proof. 對任意一張圖,  個重量函數都無法估立出最短路徑的機率是
個重量函數都無法估立出最短路徑的機率是 . 而
. 而 個點的有向圖共有
個點的有向圖共有 個, 因此
個, 因此 個重量函數都無法孤立出某一張
個重量函數都無法孤立出某一張 點有向圖的最短路徑的機率是
點有向圖的最短路徑的機率是
 ,
,
因此存在某個重量函數不管什麼樣的 點有向圖都能夠孤立出其最短路徑.
點有向圖都能夠孤立出其最短路徑. 
注意後面這個推論的重點: 那 個重量函數是對所有
個重量函數是對所有 點的有向圖都適用的, 因此我們可以把這些重量函數事先寫進程式當中, 每當輸入一個圖我們就拿其中一個重量函數來孤立出最短路徑. 如果不使用這種方式, 我們就要在程式執行過程中隨機的產生一些重量函數, 給定了一個圖, 我們需要
點的有向圖都適用的, 因此我們可以把這些重量函數事先寫進程式當中, 每當輸入一個圖我們就拿其中一個重量函數來孤立出最短路徑. 如果不使用這種方式, 我們就要在程式執行過程中隨機的產生一些重量函數, 給定了一個圖, 我們需要

個 random bits 來產生一組重量函數.
—
接下來我們來看第二種方法.
前面提到如果不限制重量的大小, 只要對 中的元素給予重量
中的元素給予重量 就好了. 第二個方法利用中國剩餘定理很輕易的將重量作一些改變而壓在多項式大小, 因此這樣的方法式建構式的. 我們回到只有一個
就好了. 第二個方法利用中國剩餘定理很輕易的將重量作一些改變而壓在多項式大小, 因此這樣的方法式建構式的. 我們回到只有一個 的狀況, 這次我們利用
的狀況, 這次我們利用 內子集的數量來減少 random bits 的使用.
內子集的數量來減少 random bits 的使用.
Theorem 2. 令 為一大小為
為一大小為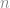 的集合, 而
的集合, 而 為一非空集合,
為一非空集合,  中每一元素為
中每一元素為 的子集. 存在一種使用
的子集. 存在一種使用 個 random bits 的方式在
個 random bits 的方式在 上給定
上給定![[n^7]](https://s0.wp.com/latex.php?latex=%5Bn%5E7%5D&bg=ffffff&fg=777777&s=0&c=20201002) 內的重量, 使得至少有
內的重量, 使得至少有 的機率會使得
的機率會使得 中正好只有一個最小重量的
中正好只有一個最小重量的 子集.
子集.
最糟糕的狀況下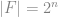 , 因此使用的 random bits 會是
, 因此使用的 random bits 會是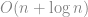 , 比前一種方法好; 當
, 比前一種方法好; 當 更小的時候 (如|F|是多項式大小), 我們甚至只需要至多$latex O(\log n)$ bits 就夠了. 完整的證明請見 [CRS93]. 不過事實上如果
更小的時候 (如|F|是多項式大小), 我們甚至只需要至多$latex O(\log n)$ bits 就夠了. 完整的證明請見 [CRS93]. 不過事實上如果 只有多項式大小, 我們其實可以連 random 都不要用! 這在 [PTV10] 裡被拿來用以證明
只有多項式大小, 我們其實可以連 random 都不要用! 這在 [PTV10] 裡被拿來用以證明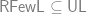 , 管它這兩個莫名其妙的東西是什麼.
, 管它這兩個莫名其妙的東西是什麼.
Theorem 2′. 令 為一大小為
為一大小為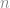 的集合, 而
的集合, 而 中有至多
中有至多 個
個 的子集
的子集 . 存在一種在
. 存在一種在 上給定多項式大小的重量, 使得
上給定多項式大小的重量, 使得 中正好只有一個最小重量的
中正好只有一個最小重量的 子集.
子集.
Proof. 首先我們給 中的每個元素
中的每個元素 重量
重量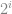 . 然後我們來看底下這個多項式:
. 然後我們來看底下這個多項式:
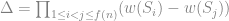 ,
,
這個多項式的特色就是: 當重量函數 能讓所有
能讓所有 中的元素重量都不一樣時, 這個判別式
中的元素重量都不一樣時, 這個判別式 就會不為零.
就會不為零.  值的範圍會是
值的範圍會是 . 因此我們選出從2開始的
. 因此我們選出從2開始的 個質數
個質數 , 使得它們相乘超過
, 使得它們相乘超過 . 換句話說,
. 換句話說,
 .
.
根據質數定理,
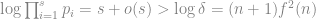 ,
,
當 時我們只要有
時我們只要有 就夠了. 這時中國剩餘定理告訴我們, 因為
就夠了. 這時中國剩餘定理告訴我們, 因為 , 所以一定有一個
, 所以一定有一個 使得
使得 . 最後我們只要令新的重量函數為
. 最後我們只要令新的重量函數為 就行了, 根據對質數大小的估計,
就行了, 根據對質數大小的估計,
 ,
,
因此這個重量函數只有多項式的大小而已. 因為 , 所有
, 所有 中的元素重量都不一樣, 滿足我們對定理的需求.
中的元素重量都不一樣, 滿足我們對定理的需求. 
最後有一些後記. Isolation Lemma 使用上需要 randomized, 因為 在最糟的狀況下會有
在最糟的狀況下會有 個元素, 因此完全的 derandomized 是不可能的. 不過針對
個元素, 因此完全的 derandomized 是不可能的. 不過針對 的特性 (例如前面舉的最短路徑的例子), 有些人致力於 derandomize 相關的結果, 也有不少成果. 希望未來能看到 Isolation Lemma 更多的應用!
的特性 (例如前面舉的最短路徑的例子), 有些人致力於 derandomize 相關的結果, 也有不少成果. 希望未來能看到 Isolation Lemma 更多的應用!
References.
[MVV87] Matching is as easy as matrix inversion. K. Mulmuley, U. Vazirani and V. Vazirani.
[CRS93] Randomness-optimal unique element isolation, with applications to perfect matching and related problems. S. Chari, P. Rohatgi and A. Srinivasan.
[RA00] Making nondeterminism unambiguous. K. Reinhardt and E. Allender.
[PTV10] On the power of unambiguity in logspace. A. pavan, R. Tewari and N. V. Vinodchandran.
演算法. 這被 Micali-Vazirani 推廣到了 general graph 上, 改進了標準的 Edmonds 開花演算法. 在這之後 Mucha-Sankowski 利用 Gaussian Elimination 及矩陣相乘作到了 randomized
time.
time, 是第一個 near linear-time 的演算法! 使用的技巧是最近正夯的 Glauber Dynamics, 分析稍微複雜, 但演算法卻是簡單的驚人!
為任意 matching. 令
.
次, 迴圈參數為
:
.
有
的機率是
, 有
的機率是
.
是個 matching, 則令
; 不然就還是讓
.
, 程式結束.
