exponential-time | Finite Playground

今天要介紹的東西是因為想著其他的問題時間接學到的. 考慮底下這樣的問題:

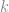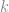$k$ -path Problem. 判斷一張無向圖 $G$ 中有沒有一條長度大於 $k$ 的 path?

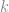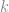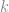看起來很單純. 我們想要討論這個問題的時間複雜度: 請問 $k$ 的大小會對問題的難度造成什麼樣的影響? 首先我們可以觀察到當 $k=O(1)$ 時, 一定會有一個 poly. time 的演算法, 簡單來說就是暴搜過所有 $k$ 個點的子集合, 檢查它們有沒有形成一條 path. 事實上, 在 Alon, Yuster & Zwick 的經典論文 “Color-coding” 當中, 就給出了 $O(M(n) \log n)$ 的演算法, 能夠判斷圖中有沒有長度為某一固定 $k=O(1)$ 的 path; 時間中的 $M(n)$ 是 $n \times n$ 矩陣相乘的時間, 與 $k$ 完全無關. 在同一篇論文中, 其實對於 $k=O(\log n)$ 長度的 path 也是能在 polynomial time 內找到的, 因為其實真正的時間長相是類似 $O^*(c^k)$ 這樣. 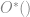( $O^*()$ 記號會吃掉所有多項式時間的部分!) 另一方面, 當 $k=n$ 時就變成了鼎鼎有名的 Hamiltonian path 問題, 我們都知道這是 $\mathsf{NP}$ -complete, 假設 $\mathsf{P} \neq \mathsf{NP}$ 的話, 是不會有 polynomial time 演算法的. 因此問題就來了:

如果我們想要解稍微大一點的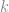 $k$ -path problem, 例如 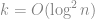$k=O(\log^2 n)$ , 有可能有多項式時間演算法嗎?

經過一陣網路上的詢問, 答案似乎是 NO. 要怎麼說明這件事呢? 我們要用到 complexity 理論裡的另一個猜想, 由 Impagliazzo 和 Paturi 在 2001 年的論文中提出的:

Exponential Time Hypothesis (ETH). 3-SAT 問題不能在 $2^{o(n)}$ 內解掉.

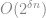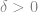這個猜想是怎麼回事呢? 我們都知道 $\mathsf{NP}$ -complete 問題能在 exponential time 解掉, 也就是 $O(2^{\delta n})$ , 對於某個 $\delta > 0$ . (基本上就是暴搜!) 但是說不定有些問題能夠在比 polynomial time 慢一些, 但比 exponential time 快一些的時間內解掉, 像是 $O(2^{\sqrt{n}})$ 之類的. 這個猜想下了一記重擊: 很多能被 3-SAT reduce 到的問題, 是都沒有 sub-exponential time 演算法的!! (注意這裡的 reduction 需要比當初證明 $\mathsf{NP}$ -hard 的 reduction 再強一點, 要保持 sub-exponential time 的性質) 因此很明顯的證明 ETH 會間接證明了 $\mathsf{P} \neq \mathsf{NP}$ . (prove it!)

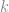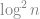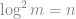所以這跟我們的 $k$ -path 問題有什麼關係呢? 我們可以證明若是對於 $\omega(\log n)$ -path 問題有個 polynomial time 解的話, 會違反 ETH!! 為了說明方便, 假設我們有個 polynomial time 演算法 $A$ 能解 $\log^2 n$ -path 問題好了. 根據 ETH, 我們可以證明 Hamiltonian path 也不能在 $2^{o(n)}$ 內解掉. 而現在若有一張圖我們想要找 Hamiltonian path, 我們先加上很多孤立點, 使得總點數有 $m = 2^{\sqrt{n}}$ 這麼多; 這時我們用演算法 $A$ 解 $\log^2 m = n$ -path 問題. 因為加上去的點都是孤立點, 所以如果找到了 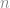$n$ -path 表示原先圖中有 Hamiltoniam path. 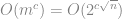而因為演算法 $A$ 是個多項式時間演算法, 我們花了 $O(m^c) = O(2^{c\sqrt{n}})$ 的時間解了 Hamiltonian path 問題, 因此違反了 ETH; 所以我們證明了 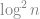$\log^2 n$ -path 問題是不能多項式時間解掉的. 同樣的理由對於任何 $\omega(\log n)$ -path 問題, 上面的敘述都保證不會有多項式時間解.

所以, 對於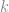 $k$ -path problem, 我們有個很棒的分界點: 當 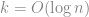$k = O(\log n)$ , 我們有多項式時間演算法; 當 $k = \omega(\log n)$ , 若 ETH 為真, 則不存在多項式時間演算法. 因此有了 ETH 世界變得很簡單! 而 ETH 還有很多的用法, 在 parametrized complexity 以及 approximation algorithm 的 lower bounds 都有用途, 以後慢慢學習!

Finite Playground

To verify is human; to prove, divine.

Tag Archives: exponential-time

MA-SETH is false

Exponential Time Hypothesis